Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
1. Традиционное введение комплексных чисел.
Вспомним, как решается квадратное уравнение выделением полного квадрата:
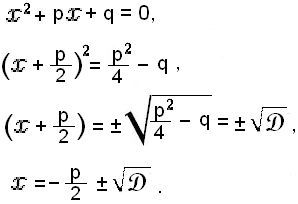
Если дискриминант 
, то есть два решения.
Если 
, то есть только одно решение.
А когда 
, нет ни одного решения.
Так было до тех пор, пока не начиналось изучение комплексных чисел. Тогда нас начинают уговаривать, дескать, существует особое число 
, такое, что i2 = –1.
Поэтому вдруг оказывается, что если , тоже есть два решения:
И приходится смириться с тем, что существуют какие-то особые числа, называемые комплексными, вида 
, где 
и 
действительные числа.
Представление комплексных чисел в виде называется алгебраической формой записи.
В прошлом математики вынуждены были оперировать комплексными числами, но относились к ним очень настороженно. Вот, например, что писал по их поводу Лейбниц в 1702 году: "Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием".
Несмотря на то, что квадратный корень из минус единицы при традиционном подходе нечто совершенно непонятное, в наше время особых психологических проблем с комплексными числами не возникает, потому что любая операция с ними оказывается в точности такой, как если бы они были обычными двучленами, где играет роль аргумента.
Единственное существенное отличие комплексных чисел от двучленов состоит в том, что квадрат корня из минус единицы везде, как он только появится, заменяется на обычную минус единицу: 
.
Далее вводится операция комплексного сопряжения комплексного числа, она заключается в том, что знак при меняется на противоположный.
Например: и 
взаимно комплексно сопряжены.
Произведение таких чисел равно действительному неотрицательному числу: 
.
Модулем комплексного числа называется следующее число:
Оно равно нулю тогда и только тогда, когда комплексное число равно нулю, т. е. при = = 0.
Действительные числа оказываются частным случаем комплексных, когда =0. Мнимые числа тоже частный случай комплексных, когда =0.
Поскольку операции с комплексными числами в алгебраической форме , выполняются в точности так же, как если бы эти числа были обычными двучленами, где играет роль аргумента, то при делении одного комплексного числа на другое применяется специальный приём:
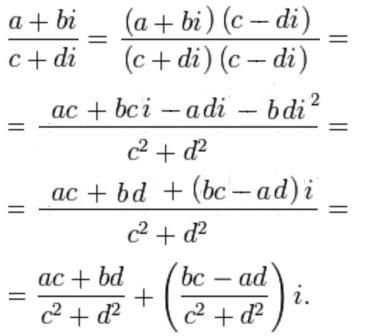
Здесь делимое и делитель умножаются на число, комплексно сопряжённое делителю, чтобы деление, в конечном итоге, выполнялось не на комплексное, а на обычное действительное число, после чего совершаются все действия согласно ситуации.
Наконец, те читатели, которые не только ознакомились с начальными свойствами комплексных чисел, но узнали значительно больше, а именно, изучили теорию комплексного переменного, наверняка получили от этого немалое удовольствие, потому что теория комплексных чисел чрезвычайно мощная, она богата возможностями. Комплексные числа вовсе не курьёз, а занимают своё достойное место в современной математике, физике и инженерии.
И, наконец, оказывается, что комплексные числа являются особыми матрицами.
Последние комментарии