Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
Математический аппарат квантовой механики, как оказалось, имеет своим истоком обычную классическую реальность.
Поэтому проиллюстрируем прямо сейчас, не обращаясь к квантовой физике, его существенные черты.
1. Независимость описания реальности от выбора систем координат.
Физическая реальность, а именно, перемещение тел, действующие силы, напряжённости электрических и магнитных полей и т.п. существуют объективно, независимо от нас.
Мы можем произвольно выбирать системы координат и, в зависимости от нашего выбора, получаем разные формулы. Но за всеми различиями в формулах скрывается объективно существующая физическая реальность. Следовательно, возможно описание реальности свободное от произвола, обусловленного выбором систем координат, короче говоря, возможно инвариантное описание реальности.
Именно на этом основана векторная (и тензорная) алгебра, причём векторы являются объектами трёхмерного евклидового, а попросту говоря, физического пространства.
Но мы знаем (см. Описание направлений и поворотов в трёхмерном пространстве. III), что направления физического пространства можно задавать через математические объекты двумерного комплексного евклидового пространства. — В связи с этим открывается ещё одна возможность инвариантного описания физической реальности.
2. Кет- и бра- векторы.
Итак, пусть имеется единичный вектор, определяющий направление какой-либо физической величины, — силы, вектора напряжённости поля, оси вращения и т.п. Этому вектору соответствует в двумерном евклидовом пространстве вектор
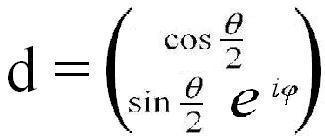 ,
,
такой, что d†d=1.
После умножения этого вектора на произвольное комплексное число с единичным модулем, матричные элементы матрицы d изменятся, но матрица d всё равно будет задавать то же самое направление (см. Описание направлений и поворотов в трёхмерном пространстве. III).
И ещё. Повернём систему координат произвольным образом. Матрицы поворота, как известно, таковы (см. Описание направлений и поворотов в трёхмерном пространстве. II):
UX(α/2) = Е cosα/2 + iσx sinα /2,
UY(α/2) = Е cosα/2 + iσy sinα/2,
UZ(α/2) = Е cosα/2 + iσz sinα/2 .
В результате получим матрицу d′ = Ud, здесь U — или одна из матриц UX(α/2), UY(α/2), UZ(α/2), или их любое произведение.
И опять, несмотря на то, что d и d′ = Ud совершенно разные матрицы, они изображают одно и то же направление (пассивная интерпретация).
Поэтому возникает естественное желание изображать всевозможные матрицы, изображающие одно и то же направление, единообразно, т.е. инвариантно, например, так: |d›.
|d› называют кет-вектором.
Поскольку матрицам d соответствуют вполне определённые эрмитово сопряжённые матрицы d†, то введём обозначение |d›† = ‹d|.
Вектор ‹d| называют бра-вектором.
В результате двойного эрмитового сопряжения любая матрица возвращается к исходному виду. И поскольку инвариантными обозначениями зашифрованы обычные матрицы, то
‹d|† = (|d›†)† = |d›,
Теперь выражение d†d = 1 можно записать в инвариантной форме:
‹d|d› = 1.
Здесь и далее идёт речь о своеобразной модификации векторного исчисления, которая была разработана выдающимся английским физиком-теоретиком Полем Дираком специально для квантовой механики.
Выражение ‹d|d› является, по сути, скобкой. По-английски скобка — bracket. Отсюда понятно, почему векторы ‹d| и |d› называются бра-векторами и кет-векторами соответственно.
То, что ‹d|d› = 1 означает, что вектор |d› нормирован на единицу, иначе говоря, норма (длина) вектора d равна единице, r = 1.
Следует подчеркнуть, что только векторы, нормированные на единицу, изображают направления в трёхмерном евклидовом (физическом) пространстве.
Известно, что угол между двумя направлениями d1 и d2 вычисляется по формуле (см. Описание направлений и поворотов в трёхмерном пространстве. VI):
cos2α/2 = (d2†d1) · (d2†d1)* = |(d2†d1)|2.
В инвариантной форме формула принимает следующий вид:
cos2α/2 = ‹d2|d1›‹d2|d1›* = |‹d2|d1›|2.
3. Гильбертово пространство.
До сих пор мы воспринимали двумерное комплексное эвклидово пространство чисто интуитивно, — оно подобно двумерному действительному евклидовому пространству с единственным отличием: координаты, а также компоненты векторов могут быть комплексными числами.
Теперь определим это понятие более чётко.
Матрицу d можно представить в следующем виде:
d = (cosθ/2)е1 + (еiφ · sinθ/2)е2 ,
здесь
е1 и е2 обладают следующими свойствами: е1Т · е1 = е2Т · е2 = 1, е1Т · е2 = е2Т · е1 = 0, или, что то же самое,
еiТ · еj = δij , i, j = 1, 2.
Здесь δij — символ Кронекера. Он равен единице, если i = j и нулю, если i ≠ j.
Сейчас, пока мы рассматриваем самые простые ситуации, введение общепринятых компактных обозначений, вроде символа Кронекера, знака суммирования и т.п., кажется неуместным. Но уже теперь пора к ним привыкать, потому что общепринятые обозначения экономны, они позволяют обобщать многие результаты на более сложные случаи с минимальными усилиями, можно сказать, автоматически.
Теперь запишем d в инвариантной форме:
|d› = (cosθ/2)|е1› + ( еiφ · sinθ/2)|е2›,
причём
‹еi|еj› = δij, i, j = 1, 2.
Обратите внимание на то, что вектор |d› нормирован на единицу, ‹d|d›=1. Именно это условие должно выполняться для того, чтобы вектор |d› задавал какое-то направление в трёхмерном евклидовом пространстве.
Определение. Множество всех векторов типа
где b1 и b 2 — произвольные комплексные числа, называется двумерным комплексным евклидовым пространством. Его также называют гильбертовым пространством, потому что если размерность пространства конечная, то двумерное комплексное евклидово пространство и (комплексное) гильбертово пространство совпадают.
В дальнейшем будем применять термин «гильбертово пространство», потому что так короче.
Векторы |е1› и |е2› составляют ортонормированный базис гильбертова пространства. «Орто-» значит ортогональный, то есть ‹е1|е2› = ‹е2|е1› = 0, «нормированный» значит нормированный на единицу ‹е1|е1› = ‹е2|е2› = 1.
Теперь вычислим
‹е1|b› = ‹е1|(b 1|е1› + b2|е2›) = b1‹е1|е1› + b2‹е1|е2›) = b 1.
Аналогично вычисляется ‹е2|b› = b2.
Итак, коэффициенты разложения любого вектора по базисным векторам гильбертова пространства равны:
bk = ‹еk|b›, k = 1, 2.
Как мы уже знаем, для того чтобы вектор гильбертова пространства изображал какое-то направление трёхмерного евклидового пространства, необходимо, чтобы он был нормирован на единицу. Итак, потребуем, чтобы ‹b|b› = 1:
‹b|b› = (b1*‹е1| + b 2*‹е2|)(b1|е1› + b 2|е2›)=
b1*· b1‹е1|е1› + b 1*· b2‹е1|е2› + b2*· b1‹е2|е1› + b 2*· b 2‹е2|е2› =
b 1*· b 1 + b2* · b 2 = |b1|2 + |b 2|2 = 1,
т.е. условие нормировки любого вектора двумерного гильбертова пространства имеет вид:
Если у вас возникают сомнения в том, правильно ли выполняются инвариантные вычисления, то вспомните, что инвариантные обозначения возникли из матричного исчисления, поэтому для них справедливы все правила действий с матрицами.
Последние комментарии