Комплексные числа и повороты на плоскости. II

Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».

Чтобы скачать полный текст, пройдите по ссылке.

Назад    Вперёд

2. О возможности особых решений квадратного матричного уравнения.

Решим квадратное матричное уравнение, где любая буква из этого уравнения представляет собой квадратную матрицу второго порядка:

,

здесь  — произведение действительных чисел  на единичную квадратную матрицу:

Наконец,  — нулевая матрица, которая отличается от Е тем, что у неё все матричные элементы нули.

Напомню, что единичная матрица при умножении матриц играет роль единицы:

— её можно умножать справа и слева на число,

— любая степень единичной матрицы равна единичной матрице, в частности, Е² = Е,

— единичная матрица, а также произведение единичной матрицы на число коммутирует с любой квадратной матрицей второго порядка.

Поэтому выделяем, как обычно, полный квадрат:

Поскольку Е² = Е, то квадратный корень из единичной матрицы равен единичной матрице. И тогда получаются решения в точности такие, как для уравнения с действительными числами.

Однако оказывается, что возможны особые решения, возникающие в связи с тем, что квадратные корни из матриц можно извлекать по-разному.

3. Двойные числа.

Пусть дискриминант матричного уравнения

положителен  , тогда

Оказывается, существуют неединичные матрицы, квадрат которых равен единичной матрице, например:

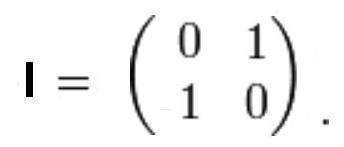
Непосредственным возведением в квадрат можно убедиться, что I² = Е.

Тогда имеем: 

А теперь то же самое, т.е. произвольное решение квадратного уравнения, но в других обозначениях:

Здесь  и  некоторые действительные числа.

Вспомним, что единичная матрица при умножении играет роль единицы, поэтому выполняя алгебраические преобразования, можно вообще её опускать, точно так же, как мы опускаем обычную единицу при вычислениях с действительными числами.

В результате получаем алгебраическую запись т.н. двойных чисел:

.

Они двойные потому, что здесь есть две единицы: обычная единица и особая единица, такая, что I² = 1 (в случае алгебраической записи вместо единичной матрицы пишем просто единицу). 

Конечно же, выражения вида  являются матрицами, но их можно считать числами в том смысле, что их можно умножать на число, складывать друг с другом, вычитать одно из другого, и даже перемножать. Умножение двойных чисел выполняется так, как если бы они были обычными двучленами, аргументом которых является особая единица, причём квадрат особой единицы всегда заменятся на обычную единицу I² = 1.

Т.е. во всём этом они аналогичны комплексным числам.

Точно так же, как в случае комплексных чисел, вводится сопряжёние двойных чисел, а затем модуль двойного числа:

Наконец, при делении двойных чисел применяется такой же приём, как при делении комплексных чисел: делимое и делитель умножаются на двойное число, сопряжённое с делителем, а затем выполняются все действия, согласно ситуации.

Но в отличие от комплексных чисел, среди которых есть лишь одно число с нулевым модулем, модуль двойных чисел равен нулю при условии, что  ; следовательно, деление на двойные числа, удовлетворяющие этому условию невозможно. Поэтому область применимости двойных чисел значительно уже, чем область применимости комплексных чисел.

Назад      Вперёд     

©   А. А. Дмитриевский.