Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
8. Синус и косинус суммы и разности двух углов.
Пусть сначала выполняется поворот на угол 
с матрицей 
, а затем на угол 
с матрицей 
. Результирующий поворот будет выполняться на угол 
с матрицей 
.
Выясним, как преобразуются координаты точки, у которой первоначально абсцисса была равна единице, а ордината нулю; соответствующая матрица имеет вид:
Координаты точки после поворота будут изображаться матрицей–столбцом 
или, что, то же самое, матрицей–столбцом 
.
Выполним соответствующие вычисления:
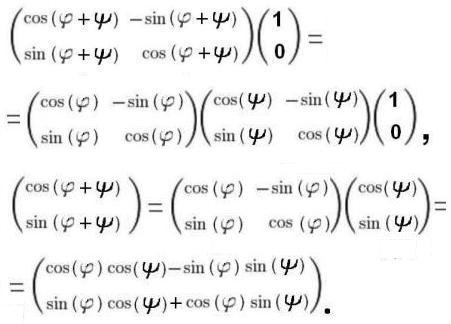
В итоге получили общеизвестные формулы для суммы косинусов и синусов двух углов:
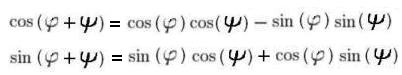
Эти соотношения можно получить ещё проще, перейдя в равенстве 
, от матричной записи к комплексным числам в тригонометрической форме:
.
Действительная часть этого равенства даёт формулу косинуса суммы двух углов, а мнимая часть даёт формулу для синуса суммы.
Обратите особое внимание на последнее выражение. Оно означает, что при перемножении комплексных чисел их аргументы складываются.
Если бы мы перемножали комплексные числа не с единичными, а с произвольными модулями, то в результате очевидного обобщения получили бы, что при перемножении комплексных чисел их модули перемножаются.
А теперь, применим полученные формулы для суммы 
:
Принимая во внимание чётность косинуса и нечётность синуса, 
, окончательно получаем:
.
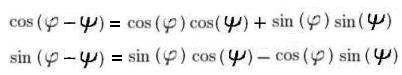9. Показательная форма комплексных чисел.
Равенство
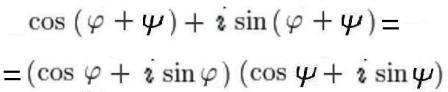
означает, что при перемножении комплексных чисел их аргументы складываются.
Точно таким же свойством обладает показательная функция:
Поэтому комплексное число является некоторой показательной функцией, причём функцией комплексного аргумента.
Оказывается, имеет место формула Эйлера:
,
здесь 
особое трансцендентное число, состоящее из бесконечного числа цифр после запятой, называемое основанием натуральных логарифмов.
Это число, а также формула Эйлера изучаются в курсе математического анализа.
Итак, любое комплексное число может быть представлено в показательной форме:
Или
здесь 
— действительное число, такое, что 
.
10. Интерпретация математических объектов.
Математические объекты и соотношения между ними являются абстракциями. Т.е. они являются результатом абстрагирования, отвлечения от конкретного содержания.
Но, применяя математику к конкретным ситуациям, приходится спускаться "с небес на землю", — наполнить математические соотношения конкретным содержанием, т.е. как-то интерпретировать математические объекты и соотношения между ними.
Возможны самые различные интерпретации одних и тех же абстракций.
Отсюда проистекает поразительная сила математики, — вроде бы делается какая-то одна работа, а её результат, вдруг, оказывается, применим в очень разных ситуациях.
Далее приводятся полезные для будущего интерпретации нескольких полученных выше формул.
Последние комментарии