Коротко о тригонометрических функциях. II

Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».

Чтобы скачать полный текст, пройдите по ссылке.

К началу

4. Обобщение тригонометрических функций на случай любых углов.

Убедитесь самостоятельно, что всё, сказанное выше о тригонометрических функциях, справедливо для ситуации, изображённой на рисунке:

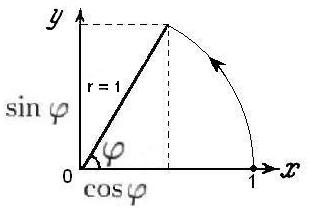
Здесь

— вершина угла φ прямоугольного треугольника совмещена с началом координат,

— гипотенуза треугольника, являющаяся также и радиусом окружности, равна единице, r = 1,

— косинус является проекцией радиуса на ось абсцисс,

— синус является проекцией радиуса на ось ординат.

Всё это правильно, но пока только для острых углов, когда радиус-гипотенуза находится в первой четверти.

Обобщение ситуации на случай любых углов очевидным образом следует из рисунка:

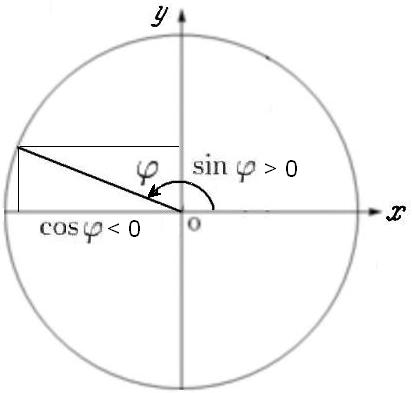
А именно, для любых углов косинус, — проекция единичного радиуса на ось абсцисс (Ox), синус — проекция единичного радиуса на ось ординат (Oy), причём в тех случаях, когда проекция попадает в отрицательную область координатных осей, функциям приписывается знак минус.

Все прочие тригонометрические функции выражаются через синус и косинус, соответствующие формулы приведены выше.

Наиболее важные свойства и графики тригонометрических функций

Функция	Область определения	Область значений	Чётность, нечётность	Период, Т	Графики функций
y  = sinx	(–∞, ∞)	[–1, 1]	нечётная	Т = 2π
y = cosx	(–∞, ∞)	[–1, 1]	чётная	Т = 2π
y  = tgx	(–∞, ∞) за исключением точек πn + π/2, здесь n целое	(–∞, ∞)	нечётная	Т = π
y = ctgx	(–∞, ∞) за исключением точек πn, здесь n целое	(–∞, ∞)	нечётная	Т = π

Функция f(x) называется чётной, если  f(–x) = f(x), и нечётной, если f(–x) = –f(x).

График чётной функции симметричен относительно оси ординат (Oy), а график нечётной функции симметричен относительно начала координат. Из графиков видно, что косинус является чётной функцией, а синус, тангенс и котангенс — нечётные.

Большинство функций не являются ни чётными, ни нечётными, они являются суммой двух слагаемых:

f(x)= [f(x) + f(–x )]/2 + [f(x) – f(–x)]/2

Первое слагаемое — чётная часть, второе слагаемое — нечётная часть.

Но основные тригонометрические функции имеют, как мы теперь убедились, вполне определённую чётность.

5. Что обязательно нужно помнить о тригонометрических функциях.

Прежде всего — обобщённое определение синуса и косинуса.

Отсюда сразу же следует, что, например, косинус в четвёртой четверти положителен, а синус отрицателен, или синус 180° равен нулю, а косинус равен минус единице. И т.п.

Полезно также уметь рисовать графики синуса, косинуса, тангенса и котангенса с обязательным указанием значений на осях абсцисс и ординат, так,  как это показано на рисунках, приведённых в таблице.

Ещё очень важные формулы:

sin²φ + cos²φ = 1.

А также

cos(φ + ψ) = cosφ  cosψ  – sinφ  sinψ,

sin (φ + ψ) = sinφ cosψ + cosφ  sinψ.

Последние две формулы можно легко восстановить из равенства:

cos(φ + ψ) + i sin(φ + ψ) = (cosφ + i sinφ ) (cosψ + i sinψ). 

Кроме того, полезно помнить о чётности-нечётности тригонометрических функций и знать их периоды.

Полезны также формулы приведения, которые позволяют выразить значения тригонометрических функций для любых углов через значения тригонометрических функций углов первой четверти.

Например:

cos(180°+ α) =  cos 180°∙ cosα  – sin180°∙ sinα  = 

(–1) ∙ cosα – 0 ∙ sinα = – cosα.

Чтобы избежать необходимости пользоваться подобными расчётами, применяют мнемоническое правило:

1. Если вычисляется тригонометрические функции углов 90° ± α или 270° ± α , то синус меняется на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс. В случае углов 180° ± α или 360° ± α  функции остаются неизменными, т.е. синус остаётся синусом и т.п.

2. Знак результата такой же, как у исходной функции в той четверти, в которую попадает исходный угол.

Например: cos(180°– α) = – cosα.

Косинус остаётся косинусом, потому что 180°, а не 90° или 270°.

Исходный угол (180°– α) во второй четверти, где косинус, исходная функция, отрицательна, поэтому знак минус.

Вот, пожалуй, и всё!

Посмотрите, сколько всяких тригонометрических формул в справочнике! Но почти все основные формулы легко получаются за одно-два действия из тех соотношений, которые мы рассмотрели.

Поэтому проще всего тригонометрические формулы не заучивать, а выводить по мере необходимости.

Конечно, не мешало бы знать тригонометрию получше, но здесь приведён необходимый минимум. Если при дальнейшем чтении что-либо понадобится дополнительно, то будут даны необходимые разъяснения. 

К началу

©   А.А.Дмитриевский.