Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
4. Представление поворотов трёхмерного пространства через половинные углы.
Оказывается, повороты в исходном трёхмерном пространстве могут быть представлены сначала некоторыми поворотами в четырёхмерном параметрическом пространстве, а затем поворотами в двумерном комплексным евклидовом пространстве.
В частности матрица

задаёт следующий поворот в параметрическом пространстве:
u1′ = u1 cosφ/2 – u3 sinφ/2,
u2′ = u2 cosφ/2 + u4 sinφ/2,
u3′ = u1 sinφ/2 + u3 cosφ/2,
u4′ = – u2 sinφ/2 + u4 cosφ/2.
Выполним соответствующие замены в формулах KS-преобразования:
|
Только результаты: |
Подробные вычисления: |
|
x′ = x |
x′ = 2(u1′ u2′ – u3′ u4′) = 2(u1 cosφ/2 – u3 sinφ/2)(u2 cosφ/2 + u4 sinφ/2) – 2(u1 sinφ/2 + u3 cosφ/2)(– u2 sinφ/2 + u4 cosφ/2) = 2(u1u2 cos2φ/2 + u1u4 sinφ/2 cosφ/2 – u2u3 sinφ/2 cosφ/2 – u3u4 sin2φ/2) – 2(–u1u2 sin2φ/2 + u1u4 sinφ/2 cosφ/2 – u2u3 sinφ/2 cosφ/2 + u3u4 cos2φ/2) = 2 u1 u2 (cos2φ/2 + sin2φ/2) – 2 u3u4 (cos2φ/2 + sin2φ/2) = 2(u1u2 – u3u4) = x. |
|
y′ = y cosφ + z sinφ. |
y′ = 2(u1′ u3′ + u2′ u4′) = 2(u1 cosφ/2 – u3 sinφ/2)(u1 sinφ/2 + u3 cosφ/2) + 2(u2 cosφ/2 + u4 sinφ/2)(–u2 sinφ/2 + u4 cosφ /2) = 2(u12 sinφ/2 cosφ /2 + u1u3 cos2φ/2 – u32 sinφ /2 cosφ/2 – u1u3 sin2φ/2) + 2(–u22 sinφ/2 cosφ/2 + u2u4 cos2φ/2 – u2u4 sin2φ/2 + u42 sinφ/2 cosφ/2) = 2(u12 – u22 – u32 + u42) sinφ /2 cosφ/2 + 2 u1u3 (cos2φ/2 – sin2φ/2) + 2 u2u4 (cos2φ/2 – sin2φ/2) = (u12 – u22 – u32 + u42) sinφ + 2(u1u3 + u2u4) cosφ = y cosφ + z sinφ. |
|
z′ = –y sinφ + z cosφ |
z′ = (u′1)2 – (u′2)2 – (u′3)2 + (u′4)2 = (u1 cosφ/2 – u3 sinφ/2)2 – (u2 cosφ/2 + u4 sinφ/2)2 – (u1 sinφ/2 + u3 cosφ/2)2 + (– u2 sinφ/2 + u4 cosφ/2)2 = u12 cos2φ/2 – 2u1u3 cosφ/2 sinφ/2 + u32 sin2φ/2 – u22 cos2φ/2 – 2u2u4 cosφ/2 sinφ/2 – u42 sin2φ/2 – u12 sin2φ/2 – 2u1u3 cosφ /2 sinφ/2 – u32 cos2φ/2 + u22 sin2φ/2 – 2u2u4 cosφ/2 sinφ/2 + u42 cos2φ/2 = u12 (cos2φ/2 – sin2φ/2) – u22 (cos2φ/2 – sin2φ/2)– u32 (cos2φ/2 – sin2φ/2) + u42 (cos2φ/2 – sin2φ/2) – 2u1u3 ∙ 2cosφ/2 sinφ/2 – 2u2u4 ∙ 2cosφ /2 sinφ/2 = (u12 – u22 – u32 + u42) ∙ cosφ – 2(u1u3 + u2u4) ∙ sinφ = –y sinφ + z cosφ |
|
r′ = r |
r′ = (u′1)2 + (u′2)2 + (u′3)2 + (u′4)2 = (u1 cosφ/2 – u3 sinφ/2)2 + (u2 cosφ /2 + u4 sinφ/2)2 + (u1 sinφ/2 + u3 cosφ/2)2 + (– u2 sinφ /2 + u4 cosφ/2)2 = u12 cos2φ/2 – 2u1u3 cosφ/2 sinφ/2 + u32 sin2φ/2 + u22 cos2φ/2 + 2u2u4 cosφ/2 sinφ/2 + u42 sin2φ/2 + u12 sin2φ/2 + 2u1u3 cosφ/2 sinφ/2 + u32 cos2φ/2 + u22 sin2φ/2 – 2u2u4 cosφ/2 sinφ/2 + u42 cos2φ/2 = u12 (cos2φ/2 + sin2φ/2) + u22 (cos2φ/2 + sin2φ/2) + u32 (cos2φ/2 + sin2φ/2) + u42 (cos2φ/2 + sin2φ/2) = (u12 + u22 + u32 + u42) = r |
Итак, получилось преобразование:
x′ = x
y′ = y cosφ + z sinφ,
z ′ = –y sinφ + z cosφ.
И, кроме того, r′ = r.
Соответствующая матрица имеет вид:
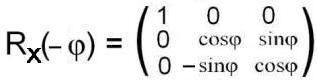
Это значит, что поворот в параметрическом пространстве, изображаемый матрицей PX(φ/2) порождает поворот в трёхмерном пространстве вокруг оси Ох по часовой стрелке (в отрицательном направлении), изображаемый матрицей RX(– φ ).
А теперь самостоятельно выполните вычисления и убедитесь, что линейные преобразования, задаваемые матричными соотношениями
![]()
и
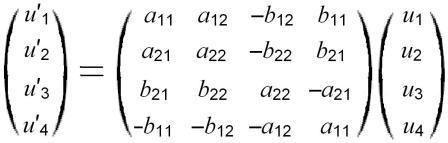
тождественны.
Отсюда понятно, что громоздкие соотношения, описывающие повороты в четырёхмерном параметрическом пространстве можно заменить более компактными эквивалентными соотношениями для двумерного комплексного евклидового пространства.
Теперь примем, что a11 = a 22 = cosφ/2, b12 = b 21 = sinφ /2, a 12 = a 21 = b 11 = b 22 = 0, и получим две эквивалентные матрицы PX(φ/2) и UX(φ/2), где
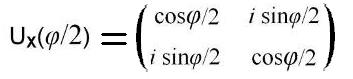 .
.
Они эквивалентны в том смысле, что задают одно и то же линейное преобразование в исходном трёхмерном пространстве.
Следовательно,
1. Матрица UX(φ/2) = Е cosφ/2 + iσx sinφ/2,
где Е — единичная матрица, а
![]()
описывает поворот в трёхмерном пространстве вокруг оси Ох по часовой стрелке (в отрицательном направлении), изображаемый матрицей RX(–φ).
Аналогично:
2. Матрица UY(φ/2) = Е cosφ/2 + iσy sinφ/2,
где
![]()
описывает поворот в трёхмерном пространстве вокруг оси Оy по часовой стрелке (в отрицательном направлении), изображаемый матрицей RY(–φ).
3. Матрица UZ(φ/2) = Е cosφ/2 + i σz sinφ/2,
где
![]()
описывает поворот в трёхмерном пространстве вокруг оси Оz по часовой стрелке (в отрицательном направлении), изображаемый матрицей RZ(–φ ).
σx , σy , σz называются матрицами Паули.
4. Матрица U0(φ/2) = Е cosφ/2 + iσ0 sinφ/2 = Е еiφ/2,
где Е — единичная матрица, а σ0 — матрица, в точности совпадающая с единичной матрицей, не описывает каких-либо поворотов в трёхмерном пространстве. Преобразование, соответствующее матрице U0(φ/2) является тождественным: x′ = x, y′ = y, z′ = z .
Доказательства утверждений 2, 3 и 4 проводится точно так же, как выше это сделано для утверждения 1. Выполните соответствующие вычисления самостоятельно, предварительно восстановив, исходя из матриц UY(φ/2), UZ(φ/2) и U0(φ/2), соответствующие им матрицы, действующие в четырёхмерном параметрическом пространстве.
Теперь рассмотрим свойства матриц поворота UX(φ/2), UY(φ/2), UZ(φ/2) на примере матрицы UX(φ/2).
Непосредственно убеждаемся, что определитель матрицы UX(φ/2) равен единице.
Квадратная матрица, у которой определитель равен единице, называется унимодулрной.
Матрицы UX(φ/2) и UX(–φ/2) взаимно являются обратными, т.к. описывают повороты в вокруг одной и то же оси, на один и тот же угол, но в противоположных направлениях, UX(–φ/2) = UX–1(φ/2).
С другой стороны, непосредственно убеждаемся, что UX†(φ/2)= (UXТ(φ/2))* = UX(–φ/2) = UX–1(φ/2), т.е. эрмитово сопряженная матрица совпадает с обратной.
Матрицы, у которых обратная матрица равна эрмитово сопряжённой, называется унитарными.
Итак, UX(φ/2) является унимодулярной и унитарной. Непосредственно проверяется, что матрицы UY(–φ/2) и UZ(–φ/2) тоже унимодулярны и унитарны.
Последние комментарии