Описание направлений и поворотов в трёхмерном пространстве. III

Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».

Чтобы скачать полный текст, пройдите по ссылке.

Назад    Вперёд

5. О неопределённости комплексной матрицы, задающей координаты точки трёхмерного пространства.

Точке трёхмерного пространства x, y, z  можно поставить в соответствие, основываясь на KS–преобразовании, комплексную матрицу

,

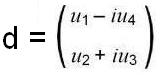и наоборот.

А теперь вспомним, что матрице поворота U₀(φ/2) = Ее^iφ/2 комплексного пространства, соответствует в трёхмерном пространстве тождественное преобразование при любом угле φ. В этом смысле матрица d и матрица U₀(φ/2) ∙ d = е^iφ/2 ∙ d фактически тождественны.

Обратите внимание, модуль числа е^iφ/2 равен единице.

Это значит, что матрица d, задающая координаты точки трёхмерного пространства, определена с точностью до умножения на произвольное комплексное число с единичным модулем.

6. Задание направлений трёхмерного пространства через половинные углы.

Выше были получены формулы, описывающие повороты в трёхмерном евклидовом пространстве через половинные углы.

Теперь рассмотрим один из способов задания направлений трёхмерного пространства через половинные углы.

Координаты в сферической системе координат естественным образом разделились: θ и φ задают направления, а r — расстояния.

И если речь идёт лишь о направлениях, то полагают для определённости r=1.

Отсюда понятно, что направления можно задавать также и декартовыми координатами x, y, z при условии r=1, или координатами параметрического пространства u₁,  u₂, u₃,  u₄ тоже при условии r=1.

Наконец, направления в трёхмерном пространстве можно также задать с помощью матрицы

,

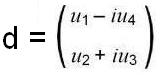где u₁,  u₂, u₃,  u₄, как известно, являются функциями половинных углов:

,

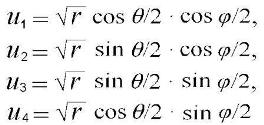причём здесь также следует полагать r = 1.

После подстановки получим матрицу, описывающую направления в трёхмерном пространстве через половинные углы:

.

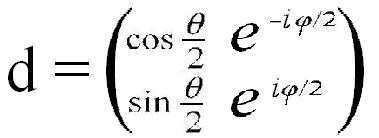Матрица d определена с точностью до комплексного множителя с единичным модулем. Поэтому домножив её на  е^iφ/2, получим наиболее часто встречающиеся выражение для матрицы, задающей направления в трёхмерном пространстве через половинные углы:

.

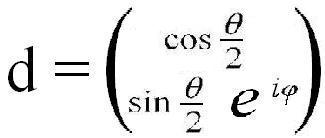7. Связь матриц Паули и KS–преобразования.

x = d^† σ_x d =

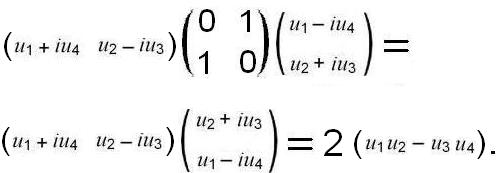
Аналогично:

y = d^† σ_y d = 2(u₁u₃ + u₂u₄),

z = d^† σ_z d = u₁² – u₂² – u₃² + u₄²,

r = d^† σ₀ d = u₁² + u₂² + u₃² + u₄².

8. Свойства матриц Паули.

8.1. Квадрат любой матрицы Паули равен единичной матрице: σ_x² = σ_y² = σ_z² = σ₀ = Е,

8.2. Определитель любой матрицы Паули равен –1.

8.3. Ещё одно важное свойство матриц Паули — их эрмитовость.

Эрмитовыми называются такие матрицы, которые сохраняются после эрмитового сопряжения, т.е. применения в любом порядке двух операций — транспонирования и комплексного сопряжения: М^† = (М*)^Т = (М^Т)* = М.

Здесь знак «†» означает эрмитово сопряжение.

8.4. Правила умножения матриц Паули:

σ_x  ∙ σ_y  = iσ_z ,

σ_y  ∙ σ_z  = iσ_x ,

σ_z  ∙ σ_x  = iσ_y .

кроме того, матрицы Паули антикоммутируют:

σ_x  ∙ σ_y  = – σ_y  ∙ σ_x ,

σ_y  ∙ σ_z  = – σ_z  ∙ σ_y ,

σ_z  ∙ σ_x  = – σ_x  ∙ σ_{z .}

Отсюда следуют коммутационные соотношения:

σ_x  ∙ σ_y  – σ_y  ∙ σ_x = 2iσ_z ,

σ_y  ∙ σ_z  – σ_z  ∙ σ_y = 2iσ_x,

σ_z  ∙ σ_x – σ_x  ∙ σ_z = 2iσ_y.

Справедливость этих соотношений легко проверяется непосредственно.

Назад    Вперёд

©   А. А. Дмитриевский.