Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
1. Описание на основе декартовых координат.
Чтобы задать направление в трёхмерном пространстве, достаточно задать декартовы координаты x, y, z какой-нибудь точки, не совпадающей с началом координат.
Луч, исходящий из начала координат и проходящий через эту точку, определит соответствующее направление.
Но чаще всего направление задаётся вектором единичной длины с компонентами (x/r, y/r, z/r), где
Теперь о поворотах.
Сразу определимся, что будем применять правую систему декартовых координат, т.е. такую, что положительное направление оси Ox совпадёт с положительным направлением оси Oy, если ось Ox повернуть на 90° против часовой стрелки, причём наблюдать такой поворот следует со стороны положительного направления оси Oz.
Тогда линейное преобразование
x′ = x ∙ cosφ – y ∙ sinφ,
y′ = x ∙ sinφ + y ∙ cosφ,
z′ = z.
будет описывать поворот любой плоскости, перпендикулярной оси Oz вокруг этой оси в положительном направлении, т.е. против часовой стрелки:
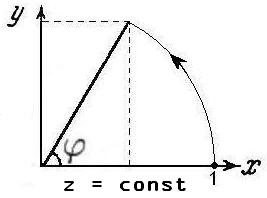
Соответствующая матрица, описывающая поворот имеет вид:
.
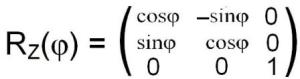Аналогично запишем поворот вокруг оси Oy:
x′ = x ∙ cosφ – z ∙ sinφ,
y′ = y ,
z′ = x ∙ sinφ + z ∙ cosφ.
Это преобразование описывает поворот в направлении от оси Ox к оси Oz, который происходит по часовой стрелке, если смотреть с положительного направления оси Oy.
Как известно, в качестве положительного направления поворота принимается поворот, происходящий против часовой стрелки. Поэтому заменим φ на –φ и, приняв во внимание чётность косинуса и нечётность синуса, получим:
x′ = x ∙ cosφ + z ∙ sinφ,
y′ = y,
z′ = – x ∙ sinφ + z ∙ cosφ.
Тогда соответствующая матрица принимает вид:
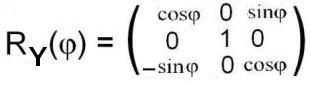
Наконец, вращение вокруг оси Ox в положительном направлении описывается линейным преобразованием:
x′ = x ∙,
y′ = y cosφ – z ∙ sinφ,
z′ = y ∙ sinφ + z ∙ cosφ.
Соответствующая матрица имеет вид:.
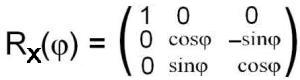
2. Сферические координаты.
Они связаны с декартовыми координатами соотношениями:
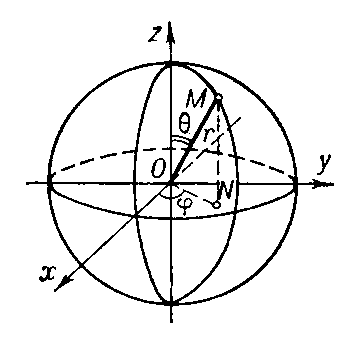
x = r sinθ cosφ,
y = r sinθ sinφ,
z = r cosθ.
Здесь — расстояние от точки М до начала координат, θ — полярный угол, который изменяется в пределах от 0 до π, φ — азимутальный угол, который изменяется в пределах от 0 до 2π.
Аналогия с географическими координатами: φ — это, по сути, долгота, а θ — угловое полярное расстояние, которое в отличие от широты отсчитывается не от экватора, а от Северного полюса Земли.
Итак, любые направления, исходящие из начала координат, определяются в сферической системе координат двумя углами, — θ и φ.
3. Переход к половинным углам. KS–преобразование.
Переход к половинным углам выполняется в соответствии с равенствами:
cosα = cos2α/2 – sin2α/2,
sinα = 2sinα /2 ∙ cosα /2.
Применим эти две формулы в подходящих обозначениях к выражениям для сферических координат:
x = r sinθ cosφ = r 2 sinθ/2 ∙ cosθ /2 ∙ (cos2φ/2 – sin2φ/2) =
= 2r(cos2φ/2 ∙ sinθ/2 ∙ cosθ/2 – sin2φ/2 ∙ sinθ/2 ∙ cosθ /2),
y = r sinθ cosφ = 4r sinθ/2 ∙ cosθ /2 ∙ sinφ /2 ∙ cosφ /2 ,
z = r cosθ = r (cos2θ/2 – sin2θ/2) (cos2φ/2 + sin2φ/2) =
= r (cos2θ/2∙ cos2φ/2 + cos2θ/2∙ sin2φ/2 – sin2θ/2∙ cos2φ/2 – sin2θ/2 ∙ sin2φ/2).
Пусть
,
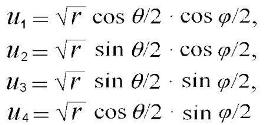тогда
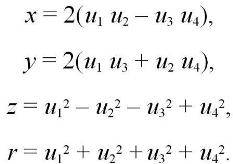
Это преобразование, называемое в небесной механике KS–преобразованием (преобразованием Кустаанхеймо-Штифеля), по-видимому, впервые было получено Хопфом в 1931 г.
Оно осуществляет переход от трёхмерного пространства с координатами точек x, y, z к четырёхмерному пространству, называемому параметрическим, с координатами точек 
.
(См. Штифель Е., Шейфеле. Г. Линейная и регулярная небесная механика. — М.: Наука, 1975, 304 с.).
Последние комментарии