§31

Итак, нам нужно доказать две теоремы.

1.

Теорема 1.

Дано:    Σ + предложение Плейфера (Σ означает совокупность всех предложений геометрии Евклида, кроме аксиомы параллельности).

Доказать

2.

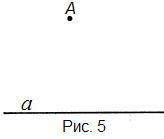Пусть даны прямая даны прямая a и точка А, не лежащая на этой прямой (рис. 5).

Можно ли построить прямую, проходящую через точку А и не пересекающую прямую a ?

3.

Как это сделать?

4.

Выполните в тетради рисунок 6.

Можно ли п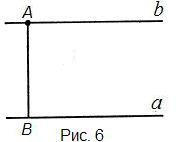остроить еще одну прямую, проходящую через точку А и не пересекающую прямую a?

Ответы.

А. Да, можно

Б. Нет, нельзя

В. Не знаю

5.

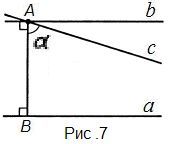Проведем через точку А прямую с под острым углом α к прямой АВ (рис. 7). Выполните рисунок.

Прямая с пересекает прямую a, так как

6.

С какой стороны от прямой АВ прямая АС пересекает прямую a?

7.

Тем самым мы доказали пятый постулат Евклида.

8.

Теорема 2.

Дано: Σ + пятый постулат Евклида.

Доказать

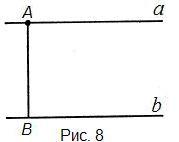Построим прямую b, проходящую через точку А и не пересекающую прямую a (рис. 8). (Это построение нами уже выполнялось при доказательстве теоремы 1.)

9.

Итак, прямая b не пересекает прямую a. Нужно доказать, что

10.

Проведем через точку А произвольную прямую c  под углом α<d к прямой АВ (рис. 9).

11.

Из сделанного построения следует, что α + β

12.

Значит, прямая c пересекает прямую a. Почему?

13.

Таким образом, любая прямая, отличная от прямой b , пересекает прямую a. Следовательно, существует единственная прямая b, не пересекающая прямую a .

Тем самым предложение Плейфера доказано.