Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
В этом сообщении приступим к рассмотрению правил действий с матрицами.
Как известно, математика возникает из реальности, — за математическими абстракциями всегда что-то стоит.
Например, 1 + 1 сколько?
—Глупый вопрос, конечно же 2!
— Однако посмотрим….
Возьмём две маленькие капли воды и начнём их сближать: 1+1. В итоге они сольются в одну каплю. Ответ: 1.
Итак, 1+1=1, это выражение справедливо, по крайней мере, для маленьких капель воды. Другое дело, что область применения этой арифметики мала, да и арифметика такая оказалась неспособной к продуктивному развитию. А вот если 1+1= 2, — то совсем другое дело.
Точно также и с матрицами.
Матрицы это просто таблицы, состоящие их чисел. Им можно приписать любые правила, лишь была бы польза и смысл.
В частности, если матрица обслуживает решение систем линейных уравнений, например, по методу Гаусса, то её строки можно менять местами, любую строку можно умножать на любое, не равное нулю число и т.п.
Здесь мы не будем вводить таких правил действий с матрицами, — нас интересует совсем другая область их применимости, поэтому и правила действий с матрицами будут другими.
В дальнейшем мы будем изучать правила действий с матрицами, которые обслуживают операции, совершаемые над линейными преобразованиями.
1. Равенство двух матриц.
Две матрицы равны, если они в точности одинаковы, т.е. содержат одинаковое число строк и столбцов, иначе говоря, их размерности одинаковы, и, кроме того, соответственные матричные элементы у них тоже одинаковы.
В противном случае матрицы будут определять различные однородные линейные преобразования, поэтому не могут считаться равными.
2. Сумма двух матриц.
Пусть даны два однородных линейных преобразования:
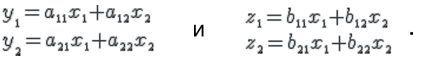
с соответствующими матрицами:
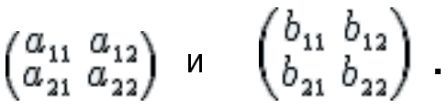
Естественно определить сумму этих двух преобразований как третье преобразование:
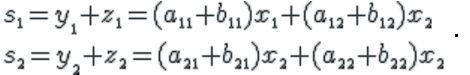
Отсюда получаем матрицу, соответствующую сумме линейных преобразований:
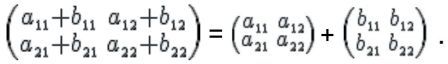
Итак, сумма матриц возможна, если матрицы имеют одинаковую размерность, т.е. одинаковое число столбцов и строк.
Матричные элементы суммы матриц равны сумме матричных элементов матриц-слагаемых.
3. Умножение матрицы на число.
Складывая две одинаковые матрицы, получим:
![]()
Продолжая аналогично, можно сформулировать правило умножения матрицы на любое натуральное число.
Естественно обобщить это правило вообще на любые допустимые числа, действительные или комплексные.
Итак, в результате умножения матрицы на число все её матричные элементы умножаются на это число:
![]()
4. Вычитание матриц.
Эта операция сводится к умножению вычитаемой матрицы на (–1), а затем к сложению получившихся матриц:
Например:
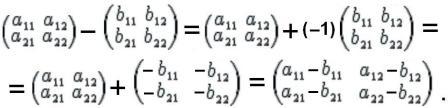
5. Транспонирование матрицы.
Операция транспонирования состоит в замене срок на столбцы и столбцов на строки, в результате чего получается новая матрица.
Это очень просто: прочитайте первую строку и запишите её в виде первого столбца, вторую строку — в виде второго столбца и т. д. и т.п.
Например:
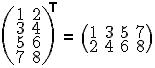
Очевидно, если матрицу транспонировать дважды, то она не изменится.
Последние комментарии